Regresión logística. ¿Por qué es tan útil? (ii)

En la anterior entrada presentábamos la regresión logística como método para modelizar la probabilidad de un suceso en función de varias variables discretas o continuas y dábamos su forma de modelización lineal:






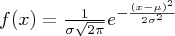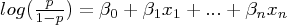
¿Por qué esta fórmula? Para contestar esta pregunta, tenemos que recordar algo que dijimos: La regresión logística no es más que un caso particular de modelo lineal generalizado, más conocidos por GLM (Generalized linear models -- no confundir con general linear models--) . En realidad estos modelos fueron planteados como una generalización de la regresión ordinaria por mínimos cuadrados y como forma de englobar diversos métodos como dichas regresiones, modelos de regresión logística o de Poisson etc.


Los GLM son métodos lineales que tratan de estimar el parámetro de una distribución de la familia exponencial (normal, Poisson, Gamma, Binomial) a través de una relación lineal y una función de enlace. Resumiendo, tenemos que un GLM consta de:

1. Distribución de probabilidad de la familia exponencial (Normal, binomial, Poisson etc)


2. Una relación lineal en la predicción


3. Una función de enlace g tal que
   

Bien, a partir de aquí ya podemos ir viendo cual es la función de enlace y establecer paralelismos con la fórmula de la regresión logística señalada arriba. Pero, ¿por qué esa función? ¿Qué es eso de la función de enlace?

Para contestar estas preguntas, ahora debemos ir al núcleo de la cuestión. La distribución de probabilidad. Ya hemos dicho que se trata de una distribución binomial, pero también hemos señalado que esa binomial es un caso particular de distribución de la familia exponencial. ¿Y eso qué quiere decir?



La familia exponencial es un conjunto de de distribuciones cuyas funciones de densidad/masa tienen un sólo parámetro y pueden expresarse (entre otras muchas equivalentes) de la siguiente manera :






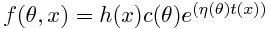
donde,

-θ es el parámetro de la familia exponencial,
-h(x) es una función real ,
-η(θ) es una función de θ. Si η(θ)= θ se dice que la función está expresada en forma canónica.
-c(θ) es otra función, que en este caso desempeña una función de normalización; Una vez se escogen las demás funciones , A sirve para normalizar la densidad y hacer que la suma o integral sobre el dominio valga 1.

-t(x) es otra función real sobre el vector de observaciones, que tiene además relación con la generación de momentos.


Todo este "lío" de funciones y parámetros puede resultar arbitrario y artificial, pero no es así y tiene aún menos de arbitrario que de artificial. Muchas de las distribuciones importantes en probabilidad cumplen esta estructura y tienen como hemos dicho importantes propiedades entre las que se encuentra el poder garantizar la obtención de un único estadístico suficiente para el parámetro poblacional θ en función a la citada función t(x).

Vamos a verlo directamente sobre la distribución binomial:



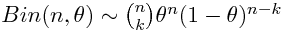
Podemos descomponer la función de masa de la binomial de la siguiente forma:




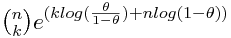
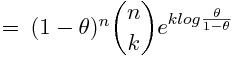
y desde aquí ver cómo podemos asimilar:






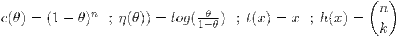
Por tanto acabamos de demostrar que la distribución binomial pertenece a la familia exponencial. Cuando el parámetro η(θ) , como hemos dicho antes , es θ (el parámetro poblacional de la distribución) decimos que la función está expresada en forma canónica. La función η(θ) , dicho de otra forma, relaciona la forma exponencial con el parámetro de la distribución , la esperanza. En el caso de una binomial, el parámetro es lo que comúnmente se denomina p. Concretando pues , la función sería:



,



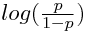también conocida como función logit , y particularmente es la inversa de la función logística en el caso típicamente conocido como sigmoide.


Después de todo esto , volvamos al principio del artículo y veamos la definición de la ecuación del modelo de regresión logística. Efectivamente aparece la función logit relacionada con los términos independientes. Ésa es nuestra función de enlace. En principio , cualquiera puede ser función de enlace , siempre que esté comprendida en el intervalo del parámetro a considerar (en nuestro caso la p de una binomial debe estar siempre entre 0 y 1). De hecho otro caso particular de GLM con la distribución binomial son los denominados modelos probit, que utilizan como función de enlace la inversa de la densidad de una normal estándar. No obstante, se suele utilizar como enlace la función canónica de cada distribución a modelizar , por ser la función que conecta el parámetro natural de la forma exponencial con su esperanza, que es lo que tratamos de modelizar.

Invito a los lectores a buscar los casos particulares de GLM con otras distribuciones, como Poisson , o la densidad normal, y ver las funciones de enlace asociadas. En el caso normal, por ejemplo , resulta que la función de enlace es la identidad, además , claro, aquí no hace falta hacer transformaciones en el dominio de valores de E[Y], ya que pueden pertenecer a toda la recta real...


Llegados a este punto hemos visto de dónde sale la formulación del modelo y su evidente utilidad para estimar proporciones , dado el caso de la distribución binomial. También hemos dado pistas para relacionar todo esto con su generalización a otras distribuciones. Si tenemos una distribución de Poisson , nuestra regresión irá encaminada a estimar su parámetro λ, típicamente el número de eventos ocurridos en una unidad de tiempo. Por cierto, véase que en este caso la función de enlace debe ser >=0..

Lo único que resta es ver cómo estimar los parámetros del modelo. Para el caso que no ocupa, este paso no se resolverá como en la regresión lineal, por el método de mínimos cuadrados, ya que ahí poníamos como hipótesis que la distribución de los errores fuera normal. Ahora no podemos hacer eso, ya que los valores observados Y son discretos y su distribución no es normal.




Los parámetros se hallarán pues a través de la estimación de máxima verosimilitud, que consiste en encontrar los parámetros β que maximizan el log de la función de verosimilitud. Recordemos que la verosimilitud puede entenderse como una función que permite establecer inferencias sobre un parámetro dada una serie de observaciones. Se trata en nuestro caso de tomar en la función de masa el parámetro p como incógnita y el valor x como observado, una "especie de versión no bayesiana" de la estimación en probabilidades condicionadas del enfoque bayesiano. Se toma el logaritmo, ya que hay que encontrar el máximo de esta función y es más sencillo calcularlo a través de logaritmos. Ya sabéis que para maximizar una función hay que tomar derivadas respecto del parámetro y ver que la segunda derivada sea <0.>





Posteriormente, una vez estimados los parámetros , hay que evaluar la bondad del ajuste y la validez del modelo, evaluar colinealidades, etc. También tenemos que decidir acerca del modo de entrada de variables en el modelo, pudiendo , igual que en regresión lineal, realizar opciones forward, backward, stepwise.. aunque de momento lo dejaremos fuera de este artículo, que no tenía la pretensión de explicar el análisis estadístico en sí, del cual se pueden encontrar miles de sitios con muy buena información, sino su origen y el porqué de su formulación. Espero sinceramente haberlo conseguido. Salimos hasta la próxima entrada.

Software estadístico- R - Trabajar con grandes conjuntos de datos. (II)

En la anterior entrada veíamos cómo importar un fichero de 4,7 Gb y un buen número de variables a un archivo legible en R. Se hacía a través de varios pasos y el uso de dos librerías adicionales , filehash y colbycol

Ahora vamos a importar el mismo fichero a través de la librería ff . Podéis ver detalles de sus instrucciones aquí.

La librería ff proporciona un medio de almacenamiento plano y de acceso rápido, proporcionando vistas físicas y virtuales de los datos. Uno de los objetos disponibles en esta librería se llama ffdf y es un análogo al data frame de R. A uno de estos objetos vamos a importar nuestro fichero a través de la función read.table.ffdf, construida para ser muy similar al read.table y almacenar ficheros con varias columnas (variables) en formato data frame, entre otras aplicaciones.

Una instrucción correcta para importar nuestros datos será por ejemplo:

>base_fichero<-read.table.ffdf("/home/datos/fichero1.txt",sep='|',fill=TRUE,x=NULL,first.rows=1e5,next.rows=8e5)

No comentaré opciones tradicionales de R(aquí las podemos meter cai todas sin problemas) , pero sí las nuevas:

-x=NULL se pone para indicar que nuestros datos no serán anexados a nada. Si tuviéramos otro ffdf y quisiéramos anexar, lo indicaríamos aquí.

-first.rows=1e5: La función read.table.ffdf lee "a trozos". Y el primer "trozo" a leer es importante porque desde aquí se toman datos relativos a factores, tipos de datos , valores etc. Por defecto, lee 1000 casos. En nuestro caso es mejor poner más para el correcto cálculo de niveles en los factores. Decir que esto se podrá recalcular posteriormente.

-next.rows=8e5: Después de la primera lectura , la función leerá y escribirá porciones del fichero original para irlos almacenando en los ficheros físicos que maneja. En esta opción se especifica el número de líneas a ller en cada pasada. Si se dispone de cierta capacidad de RAM (en mi caso unos 3Gb libres) , conviene dar manga ancha a este parámetro, puesto que redundará en mayor rapidez al disminuir el trabajo I/O.

Hay bastantes más opciones y quizá más eficientes. Pero deciros que con esto , soy capaz de leer todo el fichero original en un tiempo bastante razonable, y de una sola tacada. Es por tanto éste un método mejor que la combinación de filehash+ colbycol.

Para el uso de los datos veremos la manera de tomar los datos de una variable, denominada campo1 (ocupa la primera columna del fichero) de nuestro ffdf base_fichero:

>vector_campo1<- base_fichero[,1]
>vector_campo1<- base_fichero[,"campo1"]

Estas dos instrucciones realizan la misma labor, asignar a vector_campo1 los valores de la citada variable. El acceso a los datos de un ffdf se realiza con notación "matricial" [filas,columnas], por índice o por nombre. Si deseamos omitir filas o columnas , como en el ejemplo , simplemente se omite.

Otra posible acción es la siguiente:

>ajuste<-lm(base_fichero[,"campo1"]~ base_fichero[,"campo2"]

Y.... ahora igual que la otra vez, el sistema se queda sin memoria. Ya trabajamos en modo R clásico, poniendo los procesos en RAM . En las siguientes entradas referentes a esta serie veremos métodos para hacer análisis lo más acertados posible teniendo en cuenta esta adversidad.

Salimos..

Software estadístico- R - Trabajar con grandes conjuntos de datos. (I)

En mi interés por trabajar en entornos fuera de los comercialmente afianzados, y disponibles sólo en grandes empresas, debido fundamentalmente a su coste, llegue a conocer R.

R es un entorno de análisis estadístico donde, uno, aparte de su estructura digamos, común, puede encontrar multitud de paquetes detinados a conexión con sistemas de base de datos, tratamiento de datos y todo tipo de procedimientos estadísticos y matemáticos. Básicamente nos movemos en una línea de comandos desde donde damos instrucciones ordenadas de qué queremos hacer, modo consola de SO. Dispone también de librerías como RCommander para trabajar en un entorno gráfico que ataja algunos de esos comandos.

Al poco tiempo de empezar a documentarme sobre el entorno pude ver cómo era un problema recurrente y ya extendido en el tiempo la dificultad de trabajar con grandes volúmenes de datos. ¿Por qué? Muy sencillo. R trabaja con los datos cargados en memoria. Por lo que el conjunto de datos con el que trabajamos debe ser como mucho inferior a la memoria que tengamos libre. Esta es una limitación muy seria en mi opinión si se quiere tratar de tomar R como un entorno serio, puesto que cada vez tenemos que enfrentarnos a colecciones de datos mayores y más complejas, cuando no llegar directamente a trabajar sobre textos, etc

En este proceso de búsqueda acabé en esta magnífica página/proyecto al que deseo francamente larga vida: Análisis y decisión.

Aquí pude encontrar este artículo tres fracasos y medio con R donde se dan detalles del problema. A partir de aquí me decidí a tratar de alguna manera de abordar esto, o directamente no seguir interesándome mucho por un entorno que no ofrece mucha posibilidad de superar este inconveniente.

Una vez vistas algunas vías de salida, me decidí a investigar un poco en serio dos paquetes diseñados para alojar datos en disco, en vez de en RAM y por tanto son escalables; Los paquetes ff y filehash. Empezaremos por este último. Podéis obtener información (no muy extensa, pero suficiente) aquí. Básicamente y sobre el papel esta librería ofrece la posibilidad de trabajar directamente con bases de datos o ficheros alojados en el disco duro, sin necesidad de alojar todo en memoria.

La diversidad de documentación o ejemplos de uso variados de este paquete es más bien escasa, por lo que me lancé a la aventura para ir aprendiendo sobre la marcha. La idea es cargar un fichero de más de 40 variables con casi 10.000.000 de registros, en toal 4.7 GB. La RAM de mi equipo es de 4GB.
Filehash crea bbdd orientadas a clave, y tiene pocas pero simples funciones posibles. Una de ellas carga data frames en ficheros en disco duro.

La instrucción es directamente
> dumpDF(read.table("c:\fichero.txt",header=TRUE,sep="|";fill=TRUE),"basedatos")

Esto lee los datos de un fichero y los carga directamente en una bbdd filehash de nombre "basedatos". Aunque en algunos textos alumbran que esto se hace directamente a disco, no es cierto. Es proceso lee el fichero normalmente (a memoria) y por tanto falla.

Segunda opción: Partir nuestro fichero en pongamos 5 ó 6 ficheros de la misma estructura con menos datos. La idea sería cargar un fichero , liberar memoria, y anexar los siguientes, repitiendo el proceso. Intento inútil porque no fui capaz(no sé si se podrá hacer) de anexar nada a la base de datos. No funcionan las cosas que podrían hacerse con un dataframe, porque no lo es y la función dbInsert de filehash parece que sólo carga claves (columnas o variables, vamos). Tampoco sirve cargar tal cual, porque sustituye lo anterior.

Tercera opción: Dado que parece que se pueden insertar vectores completos, pues la respuesta está en el ar´ticulo que puse arriba . Utilizo el paquete colbycol , me desagrega el fichero original en vectores individuales. Ahora sí, tiene sentido untilizar la función dbInsert

-primero leemos el fichero con colbycol
> data<-cbc.read.table("f:/fichero.txt",header=TRUE,sep="|",fill=TRUE)
-creamos la bbdd filehash
> dbCreate("vacia")
> bvacia<-dbInit("vacia")
-ahora probamos a insertar vectores extraidos por el colbycol, de diversos modos

> dbInsert(bvacia,"CAMPO1",CAMPO1)
> dbInsert(bvacia,colnames(data)[1],cbc.get.col(data, 1 ))
> dbInsert(bvacia,"CAMPO1",cbc.get.col( data, 1 ))



Estas tres instrucciones hacen lo mismo, insertan el vector correspodiente al primer campo del fichero desmenuzado por colbycol.
En principio hice las pruebas con 6 ó 7 campos por separado y lo cierto es que fue bien en todos menos en uno de ellos, sospecho que por algún tema de memoria, ya que tenía en sistema muy cargado (no había limpiado nada y había hecho muchas pruebas de lecturas etc.) y el vector era un campo de texto (factor).

En este punto, la táctica será utilizar el número de campos del fichero como variable contador para extraer el nombre e información de los vectores y cargar todo de un tirón:
>NUMBER=ncol(data)
>for (i in 1:NUMBER){CONTENT= cbc.get.col(data, i )
+NAME=colnames(data)[i]
+dbInsert(bvacia,NAME,CONTENT)
+rm(NAME)
+rm(CONTENT) }

Esto, aunque es lento funciona. Os preguntaréis quizá por qué asigno las columnas a variables intemedias. El caso es que hacerlo directamente me resultó más lento, no sé si por que lo es, o porque en ese momento el sistema estaba más cargado. He de decir que estas pruebas no están hechas en un entorno profesional, sino en un PC casero con aplicaciones p2p, firefox, antivirus y sobre windows. Tengo pendiente testar esto en Ubuntu server , sólo dedicado a estos menesteres.

Bien, eso de arriba crea una base de datos en disco que siempre podremos recuperar mediante la asignación a un objeto:

>bvacia<- dbInit("vacia")


Para trabajar con esta bbdd , se utiliza la función with, por ejemplo, nada más tener los datos, probé:

>media<-with(bvacia,mean(campo3)) , con éxito, pero al hacer:
>with(bvacia,lm(campo3~campo8))

volvemos al principio, aunque con lo aprendido por el camino. Aquí, R comienza a actuar normalmente y traslada los datos a RAM, llegando al error "Reached total allocation of xxxxx" . Bueno al menos siempre podremos tomar muestras y analizar..

El próximo paso del que les daré cuenta será testar la librería ff , también existente con el propósito de alojar datos en disco, si bien esta promete más rapidez e incluso integración con métodos estadísticos de R, como biglm.

Salimos hasta la próxima entrada.

Regresión logística. ¿Por qué es tan útil? (i)

En esta nueva serie de artículos vamos a tratar de profundizar en un método estáditico de "modelización" muy común y útil en multitud de campos y disciplinas.La regresión logística.

La regresión logística es una técnica utilizada para resolver problemas de modelización cuando nuestra variable independiente Y es categórica y representa la ocurrencia de un suceso en particular. Lo más normal y el caso que estudiaremos se refiere a variables independientes dicotómicas, auque si dicha variable presenta más de dos categorías , habría que tomar como objeto la regresión logística multinomial. Hay que decir que a diferencia de otros métodos multivariantes , la regresión logística admite variables dependiente continuas y categóricas. Y como última observación, aunque ya veremos por qué, este método no es más que una particularización de los denominados GLM (modelos lineales generalizados), que relacionan una variable dependiente con la combinación lineal de otras dependientes a través de una función de enlace.

El objetivo pues será modelizar la probabilidad de ocurrencia de un suceso en función de la aparición de una serie de factores. Tal como hemos dicho nuestra variable Y tomará dos valores y presentará pues una distribución de Bernoulli, siendo su función de masa:



de manera que representamos con el valor 1 el éxito con probabilidad p de que ocurra y con 0 el no-éxito con probbabilidad 1-p. La regresión logística tiene por última finalidad la de poner en relación dicha variable dicotómica con otras variables y así poder estimar E[Y/x], es decir hallar el valor de p cuando se dan una serie de factores condicionantes. Además pensad en qué cantidad de problemas y situaciones en la vida real se puden modelizar de esta manera...

Imaginemos un caso práctico. Sabemos que en una determinada población hay una tasa en cierta enfermedad del 0.09%. Pero sabemos que el sobrepeso aumenta mucho el riesgo de padecer la dolencia. Si no disponemos de esta información, no podemos decir nada acerca de la probabilidad de un individuo con sobrepeso. Sin embargo si sabemos que un individuo efectivamente tiene sobrepeso , podremos como mínimo asegurar que tiene un riesgo mayor de padecer la enfermedad. Si tomamos una muestra y vemos que esto es así con una determinada probabilidad , podremos entonces para otra muestra o la población , inferir la probabilidad de un individuo en función de si presenta o no sobrepeso.

Hay numerosas técnicas estadísticas y computacionales para resolver o modelizar este tipo de problemas. Aunque en cada problema siempre hay que considerar distintas alternativas de modelización, a menudo la regresión logística se presenta como uno de los mejores o el emjor método para resolver el problema. Veamos a continuación la formulación de la regresión logística:



o de manera equivalente:

siendo p=E[Y/X=x_i].

Obviamente p será la probabilidad de ocurrencia del evento (en nuestro caso el padecer la enfermedad) y las x_i serán los factores dependientes, en nuestro ejemplo la observación de sobrepeso.

Bien , ya sabemos que mediante este modelo podemos a partir de cierta información , inferir la probabilidad de que suceda algo, a través de una fórmula un tanto extraña donde el número e (qué raro) y por tanto el Ln aparecen involucradas. Y aunque el ejemplo del sobrepeso y la enfermedad es un tanto ingénuo, la utilidad de estos métodos sale a la luz cuando tenemos muchos factores involucrados y poca información de cómo influyen el la ocurrencia o no de un determinado suceso.

En las próximas entradas sobre el tema veremos qué pinta ahí el número e, qué es la función logística, la transformación logit y qué papel juega en todo esto la familia exponencial. ¿El objetivo? Como siempre, explicar el por qué de las cosas.

Salimos hasta la próxima entrada.

Distribución Normal, campana de Gauss y algunas condusiones (y iii)

Con esta daremos por terminada la serie de entradas dedicadas a la distribución Normal y el porqué de su importancia y popularidad. Esta última parte de está dedicada a demostrar formalmente (aunque espero no sea por ello tedioso) lo que vimos en la anterior entrada, es decir, que adición de v.a.i.id sigue una distribución normal cuando tomamos muestras de n elementos siendo n suficientemente grande (n>30 comunmente). Decíamos por ello que mcuhas magnitudes observadas en la naturaleza , fruto de la adición de numerosos factores donde interviene el azar, nos permite explicar porqué se observan distribuciones aproximadamente normales muy frecuentemente.


A pesar de la gran importancia del Teorema Central del Límite , su demostración, aunque obviamente no es un juego de niños, tampoco resulta muy complicada. Para su demostración no obstante necesitamos de una herramienta básica. La función característica.

Se define la función característica de una distribución de probabilidad como :

, donde E representa la esperanza matemática e i la unidad imaginaria. La función característica de la distribución normal vendrá de integrar su densidad multiplicada por
. Esto resulta (no voy a desarrollar el cálculo) en , que será la función característica de la distribución Normal. Pero ahora muchos se preguntarán..¿pero qué es esto? ¿por qué este churro? Voy a resumir mucho y os diré que la función característica es muy importante entre otras cosas por (1), siempre existe para cualquier v.a. X y (2) ser la base de un teorema fundamental en todo esto: El teorema de continuidad de Lévy, que a groso modo nos dice que dada una sucesión de variables aleatorias X_n con funciones características φ_n(t), Si dichas funciones convergen a una función φ(t) , entonces X_n convergen a una variable aleatoria X , con función característica φ(t). Este resultado es muy importante y es utilizado tanto para el TCL como para otros lema importantes en estadística, como la ley débil de los grandes números. El reconocimiento de una función característica en una demostración será la clave en todo esto.

Bien, vamos al grano, a la demostración del TCL. En primer lugar , partimos de una v.a. X con media μ=0 y desviación típica σ=0. Su función característica será con y siendo o una función que hace tender t a 0. ¿Por qué? Esto viene del desarrollo de la función característica por Taylor, que en concreto parte de expresar la expresión en función de senos y cosenos y desarrollar por Taylor. No nos detendremos en esto, el objetivo era no liarlo demasiado.

Ahora ya tenemos nuestra v.a. con media 0 y varianza 1 y su función característica. Ahora supongamos X₁..X_n v.a. de media μ y desviación típica σ consideraremos S_i como (x_i-μ/σ)

, es decir estandarizamos las v.a. Sea entonces S_n la media de estas observaciones estandarizadas, es decir,

, ya que la media del estimador promedio es μ=0 y su desviación típica es , donde σ es 1.


Vamos ahora a calcular la función característica de S_n, recordando algo importante, y es que la función característica de la suma de dos variables es el producto de sus funciones características. Así tendremos el producto de funciones características , que por el desarrollo de Taylor que vimo antes es:




que tiende a cuando n tiende a infinito. ¿Por qué? Porque
es efectivamente el número e.


y TACHANNNN! Resulta que ésta es la función característica de una distribución N(o,1)!!! ¿Os acordáis de ese tal Lévy y su teorema de continuidad?? Efectivamente, si las funciones características son iguales, las distribuciones son iguales, y así q.e.d.

Salimos hasta la próxima entrada.

Distribución normal, campana de Gauss y algunas confusiones(ii)

Se sabe que mucho de lo que pasa y somos tiene relación con la probabilidad y la estadística. Desde cuánto medimos a la evolución del clima en Indonesia están por un lado sujetos a cierta grado de incertidumbre y por otro son susceptibles de ser observados y medidos.

De entre muchas de las cosas que cumplen las dos anteriores condiciones, hay una gran parte cuya medición utiliza una escala real y contínua. Los sueldos, el peso, la estatura, el consumo energético, el error en micras en la fabricación de un tornillo y podríamos seguir ad infinitum. Cuando observamos estas magnitudes en muchas mediciones (sujetas en algún momento al "azar") tenemos una sucesión de variables aleatorias. Tendremos distintas medidas para cada medición. Cada una dependerá de muchos factores que los harán variar de una a otra.

Bien , aquí viene el objetivo de esta serie de artículos. Resulta que cuando uno estudia o lee acerca de la distribución Normal o Gaussiana se le suele decir que este tipo de magnitudes (o la colección de mediciones) tiende a una normal con unos determinados parámetros. ¿Por qué? ¿por acto de fe? ¿es esto cierto?

Bien, en la realidad ninguna magnitud poblacional contínua tiene una distribución teórica a priori, a menos que sea un experimento no afectado por el azar. Ni sueldos, ni estaturas, ni pesos tendrían en principio por qué seguirla. Pueden ser normales , pero podrían no serlo. Ahora bien, si lo que hacemos es extraer muestras , entonces los valores de esa muestra , de alguna manera, sí. Si lo que medimos lo expresamos en función de "cúmulos" de azar, entonces podemos empezar a ver la luz. Tiene una explicación, un tanto compleja, pero que intentaré resumir de la manera más sencilla posible.

Empezaremos por el final, por el teorema que da forma a la demostración de nuestra tésis. Este es el Teorema Central del Límite (TCL). A partir de una serie de resultados previos, este lema enuncia que la suma (consecuentemente el promedio) de una gran cantidad de variables aleatorias (en adelante v.a.) sigue una distribución Normal. ¿Las condiciones? Media y variabilidad finitas. Ya vemos cómo aparece la observación de muchos datos y la distribución normal.

Aclararemos eso de la suma de v.a. Consideremos X₁,X₂,..,X_n una muestra de la población , por ejemplo la estatura de n niños de 10 años de un mismo colegio. Lo que dice el TCL es que a medida que ese n es grande , el promedio de alturas sigue una distribución Normal. Es decir, si cogiéramos varias muestras de por ejemplo 15 alumnos y calculásemos la media de altura, esas medias seguirían una distribución Normal independientemente de cual fuera la distribución de probabilidad original. En concreto el promedio de estas alturas seguirá una N(μ,σ²/n) donde μ es la media poblacional y σ² es la varianza de la población.

Visto el concepto del TCL , podemos aclarar porqué muchas magnitudes que se dan en la naturaleza siguen una distribución aproximadamente normal. Si algo se produce por acumulación de muchos factores provinientes del azar y el conjunto de estos factores es el mismo, podemos de lo anterior inferir que cada medición es el resultado de la suma de muchas v.a. idénticamente distribuidas, que como hemos visto converge una distribución Normal.

Según lo ve un servidor, es más bien que observamos una normal en los pesos y deducimos que su distribución está condicionada por muchos factores aditivos determinados por el azar. El resultado de convergencia a eso que llamaos normal es algo teórico, lo observado y su similitud , algo práctico. Como lo observado parece similar a lo teórico, llegamos a las hipótesis. Es muy difícil asegurar si no, que el peso de los habitantes de un pueblo tiene una distribución Normal "per se".

Para terminar os pondré una gráfica vista en el estudio Variación del peso durante el primer mes de vida en recién nacidos de término sanos con lactancia materna exclusiva


























Nada más que añadir. En la siguiente y última entrega veremos la demostración formal de todo esto.

Salimos hasta la próxima entrada. Para seguir el artículo podéis ir aquí.

Distribución normal, campana de Gauss y algunas confusiones(i)

Esta entrada, que será primera parte de una serie de entradas, la vamos a dedicar a la más normal de las distribuciones de probabilidad, aquella que se representa con la campana de Gauss y que parece estar detrás de la estructura y composición de muchas cosas en las que el azar interviene. Al traducir al lenguaje matemático no encontramos a menudo con la denominada distribución Normal.

Durante mis estudios y todavía hoy siento gran interés por saber el porqué de ciertas cosas que se dan por sentadas. Todo el mundo sabe por ejemplo que los barcos flotan, pero no todo el mundo sabe realmente por qué. Este ejemplo puede ser un poco infantil, pero quizá refleja el objetivo de este artículo.

El caso es que adentrándonos ya en la estadística y la probabilidad , desde muy pronto se nos plantea que muchas distribuciones , expresadas en suma o sucesión acaban como por arte de magia siendo una distribución normal y se nos dice que de manera "natural" pesos, estaturas, sueldos siguen una distribución normal,e incluso para muchos análisis de datos, normalmente de varias variables, solemos suponer "normalidad" , casi dando por sentado que una sucesión de datos tendrá esta distribución.

Pero realmente, ¿cuál es el fundamento de esto? Veremos como no todo lo dicho en el párrafo enterior es cierto. En concreto se asocia muchas veces la normalidad de ciertas magnitudes como el peso o la estatura , pero eso no quiere decir que sea así "por ley". Sin embargo, sí es cierto que la suma o el promedio de alturas y pesos siempre lo son.

No obstante es cierto que muchas magnitudes se distribuyen como una Normal. Pero, ¿Qué es exactamente una distribución normal? .Se dice que una variable aleatoria sigue una distribución normal cuando su función de densidad es:




donde μ representa la media y σ la desviación típica. Esta función fué descubierta por Carl Friederich Gauss y en su honor es comunmente denominada , entre otros nombres, como "campana de Gauss". En wikipedia podemos encontrar este gráfico de cuatro funciones de Gauss , donde varían μ y σ

















Como véis se trata de una distribución continua y simétrica, donde la media , la mediana y la moda son el mismo punto, justo la "cima" de la montaña. El parámetro μ determinará el punto central de la función (media de la v.a.) y σ determinará lo "achatada" o "picuda" que sea la gráfica. σ es la desviación típica, una medida de dispersión de los datos con respecto a su media. A mayor dispersión, más achatada será la campana, y a menor desviación, más agrupados estarán los datos en torno al centro de la curva.

Bueno, por ahora ya sabemos algo de esta distribución de probabilidad tan tan útil y popular. En las siguientes entregas nos adentraremos ya en ver el porqué de tanta popularidad y por qué algo tan aparentemente raro es tan común...

Hasta entonces, salimos hasta la próxima entrada. Para seguir el artículo podeís ir aquí.