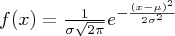Regresión logística. ¿Por qué es tan útil? (i)

En esta nueva serie de artículos vamos a tratar de profundizar en un método estáditico de "modelización" muy común y útil en multitud de campos y disciplinas.La regresión logística.

La regresión logística es una técnica utilizada para resolver problemas de modelización cuando nuestra variable independiente Y es categórica y representa la ocurrencia de un suceso en particular. Lo más normal y el caso que estudiaremos se refiere a variables independientes dicotómicas, auque si dicha variable presenta más de dos categorías , habría que tomar como objeto la regresión logística multinomial. Hay que decir que a diferencia de otros métodos multivariantes , la regresión logística admite variables dependiente continuas y categóricas. Y como última observación, aunque ya veremos por qué, este método no es más que una particularización de los denominados GLM (modelos lineales generalizados), que relacionan una variable dependiente con la combinación lineal de otras dependientes a través de una función de enlace.

El objetivo pues será modelizar la probabilidad de ocurrencia de un suceso en función de la aparición de una serie de factores. Tal como hemos dicho nuestra variable Y tomará dos valores y presentará pues una distribución de Bernoulli, siendo su función de masa:



de manera que representamos con el valor 1 el éxito con probabilidad p de que ocurra y con 0 el no-éxito con probbabilidad 1-p. La regresión logística tiene por última finalidad la de poner en relación dicha variable dicotómica con otras variables y así poder estimar E[Y/x], es decir hallar el valor de p cuando se dan una serie de factores condicionantes. Además pensad en qué cantidad de problemas y situaciones en la vida real se puden modelizar de esta manera...

Imaginemos un caso práctico. Sabemos que en una determinada población hay una tasa en cierta enfermedad del 0.09%. Pero sabemos que el sobrepeso aumenta mucho el riesgo de padecer la dolencia. Si no disponemos de esta información, no podemos decir nada acerca de la probabilidad de un individuo con sobrepeso. Sin embargo si sabemos que un individuo efectivamente tiene sobrepeso , podremos como mínimo asegurar que tiene un riesgo mayor de padecer la enfermedad. Si tomamos una muestra y vemos que esto es así con una determinada probabilidad , podremos entonces para otra muestra o la población , inferir la probabilidad de un individuo en función de si presenta o no sobrepeso.

Hay numerosas técnicas estadísticas y computacionales para resolver o modelizar este tipo de problemas. Aunque en cada problema siempre hay que considerar distintas alternativas de modelización, a menudo la regresión logística se presenta como uno de los mejores o el emjor método para resolver el problema. Veamos a continuación la formulación de la regresión logística:



o de manera equivalente:

siendo p=E[Y/X=x_i].

Obviamente p será la probabilidad de ocurrencia del evento (en nuestro caso el padecer la enfermedad) y las x_i serán los factores dependientes, en nuestro ejemplo la observación de sobrepeso.

Bien , ya sabemos que mediante este modelo podemos a partir de cierta información , inferir la probabilidad de que suceda algo, a través de una fórmula un tanto extraña donde el número e (qué raro) y por tanto el Ln aparecen involucradas. Y aunque el ejemplo del sobrepeso y la enfermedad es un tanto ingénuo, la utilidad de estos métodos sale a la luz cuando tenemos muchos factores involucrados y poca información de cómo influyen el la ocurrencia o no de un determinado suceso.

En las próximas entradas sobre el tema veremos qué pinta ahí el número e, qué es la función logística, la transformación logit y qué papel juega en todo esto la familia exponencial. ¿El objetivo? Como siempre, explicar el por qué de las cosas.

Salimos hasta la próxima entrada.

Distribución Normal, campana de Gauss y algunas condusiones (y iii)

Con esta daremos por terminada la serie de entradas dedicadas a la distribución Normal y el porqué de su importancia y popularidad. Esta última parte de está dedicada a demostrar formalmente (aunque espero no sea por ello tedioso) lo que vimos en la anterior entrada, es decir, que adición de v.a.i.id sigue una distribución normal cuando tomamos muestras de n elementos siendo n suficientemente grande (n>30 comunmente). Decíamos por ello que mcuhas magnitudes observadas en la naturaleza , fruto de la adición de numerosos factores donde interviene el azar, nos permite explicar porqué se observan distribuciones aproximadamente normales muy frecuentemente.


A pesar de la gran importancia del Teorema Central del Límite , su demostración, aunque obviamente no es un juego de niños, tampoco resulta muy complicada. Para su demostración no obstante necesitamos de una herramienta básica. La función característica.

Se define la función característica de una distribución de probabilidad como :

, donde E representa la esperanza matemática e i la unidad imaginaria. La función característica de la distribución normal vendrá de integrar su densidad multiplicada por
. Esto resulta (no voy a desarrollar el cálculo) en , que será la función característica de la distribución Normal. Pero ahora muchos se preguntarán..¿pero qué es esto? ¿por qué este churro? Voy a resumir mucho y os diré que la función característica es muy importante entre otras cosas por (1), siempre existe para cualquier v.a. X y (2) ser la base de un teorema fundamental en todo esto: El teorema de continuidad de Lévy, que a groso modo nos dice que dada una sucesión de variables aleatorias X_n con funciones características φ_n(t), Si dichas funciones convergen a una función φ(t) , entonces X_n convergen a una variable aleatoria X , con función característica φ(t). Este resultado es muy importante y es utilizado tanto para el TCL como para otros lema importantes en estadística, como la ley débil de los grandes números. El reconocimiento de una función característica en una demostración será la clave en todo esto.

Bien, vamos al grano, a la demostración del TCL. En primer lugar , partimos de una v.a. X con media μ=0 y desviación típica σ=0. Su función característica será con y siendo o una función que hace tender t a 0. ¿Por qué? Esto viene del desarrollo de la función característica por Taylor, que en concreto parte de expresar la expresión en función de senos y cosenos y desarrollar por Taylor. No nos detendremos en esto, el objetivo era no liarlo demasiado.

Ahora ya tenemos nuestra v.a. con media 0 y varianza 1 y su función característica. Ahora supongamos X₁..X_n v.a. de media μ y desviación típica σ consideraremos S_i como (x_i-μ/σ)

, es decir estandarizamos las v.a. Sea entonces S_n la media de estas observaciones estandarizadas, es decir,

, ya que la media del estimador promedio es μ=0 y su desviación típica es , donde σ es 1.


Vamos ahora a calcular la función característica de S_n, recordando algo importante, y es que la función característica de la suma de dos variables es el producto de sus funciones características. Así tendremos el producto de funciones características , que por el desarrollo de Taylor que vimo antes es:




que tiende a cuando n tiende a infinito. ¿Por qué? Porque
es efectivamente el número e.


y TACHANNNN! Resulta que ésta es la función característica de una distribución N(o,1)!!! ¿Os acordáis de ese tal Lévy y su teorema de continuidad?? Efectivamente, si las funciones características son iguales, las distribuciones son iguales, y así q.e.d.

Salimos hasta la próxima entrada.

Distribución normal, campana de Gauss y algunas confusiones(ii)

Se sabe que mucho de lo que pasa y somos tiene relación con la probabilidad y la estadística. Desde cuánto medimos a la evolución del clima en Indonesia están por un lado sujetos a cierta grado de incertidumbre y por otro son susceptibles de ser observados y medidos.

De entre muchas de las cosas que cumplen las dos anteriores condiciones, hay una gran parte cuya medición utiliza una escala real y contínua. Los sueldos, el peso, la estatura, el consumo energético, el error en micras en la fabricación de un tornillo y podríamos seguir ad infinitum. Cuando observamos estas magnitudes en muchas mediciones (sujetas en algún momento al "azar") tenemos una sucesión de variables aleatorias. Tendremos distintas medidas para cada medición. Cada una dependerá de muchos factores que los harán variar de una a otra.

Bien , aquí viene el objetivo de esta serie de artículos. Resulta que cuando uno estudia o lee acerca de la distribución Normal o Gaussiana se le suele decir que este tipo de magnitudes (o la colección de mediciones) tiende a una normal con unos determinados parámetros. ¿Por qué? ¿por acto de fe? ¿es esto cierto?

Bien, en la realidad ninguna magnitud poblacional contínua tiene una distribución teórica a priori, a menos que sea un experimento no afectado por el azar. Ni sueldos, ni estaturas, ni pesos tendrían en principio por qué seguirla. Pueden ser normales , pero podrían no serlo. Ahora bien, si lo que hacemos es extraer muestras , entonces los valores de esa muestra , de alguna manera, sí. Si lo que medimos lo expresamos en función de "cúmulos" de azar, entonces podemos empezar a ver la luz. Tiene una explicación, un tanto compleja, pero que intentaré resumir de la manera más sencilla posible.

Empezaremos por el final, por el teorema que da forma a la demostración de nuestra tésis. Este es el Teorema Central del Límite (TCL). A partir de una serie de resultados previos, este lema enuncia que la suma (consecuentemente el promedio) de una gran cantidad de variables aleatorias (en adelante v.a.) sigue una distribución Normal. ¿Las condiciones? Media y variabilidad finitas. Ya vemos cómo aparece la observación de muchos datos y la distribución normal.

Aclararemos eso de la suma de v.a. Consideremos X₁,X₂,..,X_n una muestra de la población , por ejemplo la estatura de n niños de 10 años de un mismo colegio. Lo que dice el TCL es que a medida que ese n es grande , el promedio de alturas sigue una distribución Normal. Es decir, si cogiéramos varias muestras de por ejemplo 15 alumnos y calculásemos la media de altura, esas medias seguirían una distribución Normal independientemente de cual fuera la distribución de probabilidad original. En concreto el promedio de estas alturas seguirá una N(μ,σ²/n) donde μ es la media poblacional y σ² es la varianza de la población.

Visto el concepto del TCL , podemos aclarar porqué muchas magnitudes que se dan en la naturaleza siguen una distribución aproximadamente normal. Si algo se produce por acumulación de muchos factores provinientes del azar y el conjunto de estos factores es el mismo, podemos de lo anterior inferir que cada medición es el resultado de la suma de muchas v.a. idénticamente distribuidas, que como hemos visto converge una distribución Normal.

Según lo ve un servidor, es más bien que observamos una normal en los pesos y deducimos que su distribución está condicionada por muchos factores aditivos determinados por el azar. El resultado de convergencia a eso que llamaos normal es algo teórico, lo observado y su similitud , algo práctico. Como lo observado parece similar a lo teórico, llegamos a las hipótesis. Es muy difícil asegurar si no, que el peso de los habitantes de un pueblo tiene una distribución Normal "per se".

Para terminar os pondré una gráfica vista en el estudio Variación del peso durante el primer mes de vida en recién nacidos de término sanos con lactancia materna exclusiva


























Nada más que añadir. En la siguiente y última entrega veremos la demostración formal de todo esto.

Salimos hasta la próxima entrada. Para seguir el artículo podéis ir aquí.

Distribución normal, campana de Gauss y algunas confusiones(i)

Esta entrada, que será primera parte de una serie de entradas, la vamos a dedicar a la más normal de las distribuciones de probabilidad, aquella que se representa con la campana de Gauss y que parece estar detrás de la estructura y composición de muchas cosas en las que el azar interviene. Al traducir al lenguaje matemático no encontramos a menudo con la denominada distribución Normal.

Durante mis estudios y todavía hoy siento gran interés por saber el porqué de ciertas cosas que se dan por sentadas. Todo el mundo sabe por ejemplo que los barcos flotan, pero no todo el mundo sabe realmente por qué. Este ejemplo puede ser un poco infantil, pero quizá refleja el objetivo de este artículo.

El caso es que adentrándonos ya en la estadística y la probabilidad , desde muy pronto se nos plantea que muchas distribuciones , expresadas en suma o sucesión acaban como por arte de magia siendo una distribución normal y se nos dice que de manera "natural" pesos, estaturas, sueldos siguen una distribución normal,e incluso para muchos análisis de datos, normalmente de varias variables, solemos suponer "normalidad" , casi dando por sentado que una sucesión de datos tendrá esta distribución.

Pero realmente, ¿cuál es el fundamento de esto? Veremos como no todo lo dicho en el párrafo enterior es cierto. En concreto se asocia muchas veces la normalidad de ciertas magnitudes como el peso o la estatura , pero eso no quiere decir que sea así "por ley". Sin embargo, sí es cierto que la suma o el promedio de alturas y pesos siempre lo son.

No obstante es cierto que muchas magnitudes se distribuyen como una Normal. Pero, ¿Qué es exactamente una distribución normal? .Se dice que una variable aleatoria sigue una distribución normal cuando su función de densidad es:




donde μ representa la media y σ la desviación típica. Esta función fué descubierta por Carl Friederich Gauss y en su honor es comunmente denominada , entre otros nombres, como "campana de Gauss". En wikipedia podemos encontrar este gráfico de cuatro funciones de Gauss , donde varían μ y σ

















Como véis se trata de una distribución continua y simétrica, donde la media , la mediana y la moda son el mismo punto, justo la "cima" de la montaña. El parámetro μ determinará el punto central de la función (media de la v.a.) y σ determinará lo "achatada" o "picuda" que sea la gráfica. σ es la desviación típica, una medida de dispersión de los datos con respecto a su media. A mayor dispersión, más achatada será la campana, y a menor desviación, más agrupados estarán los datos en torno al centro de la curva.

Bueno, por ahora ya sabemos algo de esta distribución de probabilidad tan tan útil y popular. En las siguientes entregas nos adentraremos ya en ver el porqué de tanta popularidad y por qué algo tan aparentemente raro es tan común...

Hasta entonces, salimos hasta la próxima entrada. Para seguir el artículo podeís ir aquí.

Primera entrada del blog Probabilitum.

Hola a tod@s!

Bienvenidos al blog probabilitum , dedicado al mundo de la probabilidad y la estadística. Espero encuentren interesantes los escasos pero bienintencionados artículos.

Salimos hasta la próxima entrada.